07.06.22. 9 класс. ГЕОМЕТРИЯ
07.06.22. 9 класс. ГЕОМЕТРИЯ.
Здравствуйте, уважаемые учащиеся.
Закрепление материала по теме "Векторы. Метод
координат".
Кто не знает,
в какую гавань он плывет,
для того нет попутного ветра. Сенека.
ИЗ ИСТОРИИ.
Идея координат
зародилась в древности. Первоначальное их применение связано с географией и
астрономией, с потребностью определять положение светил на небе и пунктов на
поверхности земли, при составлении календаря, звездных и географических карт.
Следы применения идеи
прямоугольных координат в виде квадратной сетки (палетки) обнаружены на стене
одной из погребальных камер Древнего Египта. Прямоугольной сеткой пользовались
и художники Возрождения.
Более чем за 100 лет до
н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар
параллелями и меридианами и ввести, теперь хорошо известные, географические
координаты: широту и долготу и обозначить их числами.
В XIV веке французский
математик Н.Оресм ввёл, по аналогии с географическими, координаты на плоскости.
Он предложил покрыть плоскость прямоугольной сеткой и назвать широтой и
долготой то,что мы теперь называем абсциссой и ординатой.
Это нововведение
оказалось чрезвычайно продуктивным. На его основе возник метод координат,
связавший геометрию с алгеброй. Точка плоскости – геометрический объект –
заменяется парой чисел (х; у), т. е. алгебраическим объектом.
Общематематическое
значение метода координат открыли и впервые выявили французские математики XVII
века Пьер Ферма и Рене Декарт. Изложение метода координат было впервые
опубликовано в “Геометрии” Декарта в 1637г. Отсюда и названия: “Декартова
система координат”, “Декартовы координаты”.
Термины «абсцисса», от латинского
abscissus – отсекаемый (отрезок на оси иксов), «ордината» от
латинского ordinatus – упорядоченный (отрезок на оси игреков) восходят к латинскому
переводу (XVI век) сочинений великого древнегреческого математика Аполлония и
были введены в употребление в 1670-1680гг. Г.В. Лейбницем. Им же абсцисса
вместе с ординатой были названы координатами.
Трудно переоценить
значение декартовой системы координат в развитии математики и её приложений.
Огромное количество задач, требовавших для решения геометрической интуиции,
специфических методов, получило решение, состоящие в аккуратном проведении
алгебраических выкладок.
Кривые и поверхности, определяемые ранее геометрически, получили описание в виде формул. Более того, рассматривая различные уравнения и изображая соответствующие линии и поверхности, математики, получили новые геометрические образы.
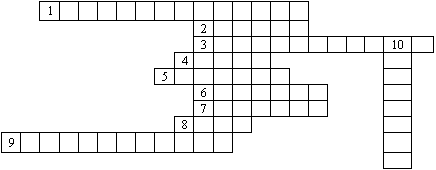
ПОВТОРИТЕ МАТЕРИАЛ ПО УЧЕБНИКУ И
РЕШИТЕ КРОССВОРДЫ.
- Коллинеарные векторы с одинаковым направлением.
- Наука, занимающаяся изучением свойств геометрических фигур.
- Вспомогательная теорема, с помощью которой доказывается следующая теорема.
- Сонаправленные векторы, имеющие равные длины.
- Коэффициенты разложения вектора по координатным векторам – это …вектора.
- Геометрическая фигура, при помощи которой складываются векторы.
- Коллинеарные векторы, имеющие равную длину, но разное направление.
- Векторы, лежащие на одной или параллельных прямых.
- Отрезок, для которого указано, какая из его граничных точек является началом, а какая концом.
- Вектор, у которого начало совпадает с концом.
- Четырехугольник, у которого противоположные стороны параллельны.
- Отрезок, для которого указано, какой из его концов считается началом, а какой концом.
- Вставьте слово “Векторы называются равными, если они… и их длины равны”.
- Вспомогательная теорема.
- Вставьте слово “Произведение нулевого вектора на любое число, считается … вектором”.
- Часть прямой, ограниченная двумя точками.
- Какая линия трапеции параллельна основаниям и равна их полусумме.
- Сколько векторов, равных данному, можно отложить от точки?
- Вставьте слово “Каждая координата … вектора на число равна произведению соответствующей координаты вектора на это число.
- Как надо учить правила и формулы по математике?
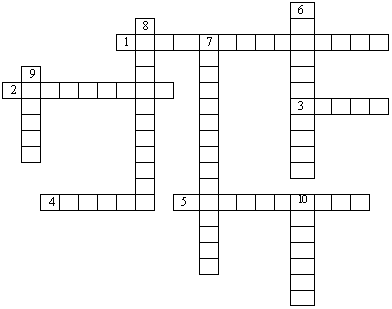

Комментарии
Отправить комментарий